Pre Algebra-regneark til skrivning af udtryk

af 05

Algebraiske udtryk Arbejdsark 1

Skriv ligningen eller udtrykket algebraisk.

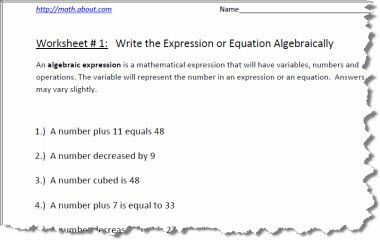
Udskriv PDF-regneark ovenfor, svarene er på den anden side.

Et algebraisk udtryk er et matematisk udtryk, der har variabler, tal og operationer. Variablen repræsenterer tallet i et udtryk eller en ligning. Svarene kan variere lidt. At være i stand til at skrive udtryk eller ligninger algebraisk er et præ-algebra-koncept, der kræves inden det tages algebra.

Følgende forkendskab er påkrævet, før du udfører disse regneark:

En forståelse af, at en variabel er et bogstav, f.eks. X, y eller n, og at det repræsenterer det ukendte tal.

At et udtryk er en sætning i matematik, der ikke vil indeholde et ligestykke, men det kan antage antagelser, variabler og betjeningstegn såsom +, - x osv. For eksempel er 3y et udtryk.

At en ligning er en sætning i matematik, der indeholder et ligestegn.

Der skal være en vis fortrolighed med heltal som er hele tal eller hele tal med et negativt tegn.

Det er også vigtigt at forstå og kende ordene: kvotient, produkt, sum, øget og formindsket, når de vedrører operationer. Når for eksempel summen bruges, skal du vide, at handlingen involverer tilføjelse eller brug af + -tegnet. Når ordet kvotient bruges, henviser det til delingstegnet, og når ordet produkt bruges, henviser det til multiplikationstegnet, der er angivet med a. eller ved at placere variablen ved siden af tallet som i 4n, hvilket betyder 4 x n

instagram viewer

af 05

Arbejdsark til algebraisk ekspression 2

Skriv ligningen eller udtrykket algebraisk.

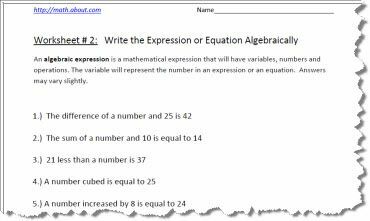
Udskriv PDF-regneark ovenfor, svarene er på den anden side.

At udskrive de algebraiske udtryk eller ligninger og få familiarti med processen er en nøgleværdighed, der kræves forud for forenkling af algebraiske ligninger. Det er vigtigt at bruge. når der henvises til multiplikation, da du ikke ønsker at forveksle multiplikation med x variablen. Selvom der findes svar på den anden side i PDF-regnearket, kan de variere lidt baseret på det bogstav, der blev brugt til at repræsentere det ukendte. Når du ser udsagn som:
Et tal gange fem er hundrede og tyve, i stedet for at skrive n x 5 = 120, ville du skrive 5n = 120, 5n betyder at multiplicere et tal med 5.

af 05

Arbejdsark til algebraisk ekspression 3

Skriv ligningen eller udtrykket algebraisk.

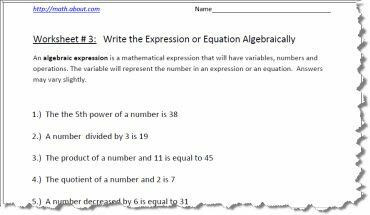
Udskriv PDF-regneark ovenfor, svarene er på den anden side.

Algebraiske udtryk kræves i læseplanen allerede i 7. klasse, men grundlaget for at udføre tas forekommer i 6. klasse. At tænke algebraisk opstår ved at bruge det ukendte sprog og repræsentere det ukendte med et bogstav. Når du præsenterer et spørgsmål som: Forskellen mellem et tal og 25 er 42. Forskellen skal betyde, at subtraktion er underforstået, og at vide, at udsagnet så ville se ud: n - 24 = 42. Med praksis bliver det anden natur!

Jeg havde en lærer, der engang sagde til mig, husk reglen om 7 og besøg igen. Han følte, at hvis du udførte syv regneark og genbesøgte konceptet, kunne du hævde, at du ville være på det punkt, hvor du forstår. Indtil videre ser det ud til at have fungeret.